Array Concepts in C++ [part 5] {insertion, deleting, search}

one dimensional array

   // 100 + i * 4

Traverse:

• • • • • • • • • • • • -

Insertion:

১/ একটা array তে কোন ভেলু insert করতে চাইলে এই কইটি ধাপ ফলো করতে হবে ।

আমরা জেটা করব সেটা হচ্ছে ইউজারর কোন ইনডেক্স এ insert করতে চাচ্ছে সেটা নিব । আপনি security এর স্বার্থে আপনি চেক করতে পারেন যে ইউজার যে ইনডেক্স দিল সেটা সঠিক কিনা না । যেমন -1, size<index এগুলা ভুল ইনডেক্স । তারপর জেটা করবেন সেটা হচ্ছে একটা লুপ চালাবেন উলটা দিক থেকে size - 1 থেকে positon পর্যন্ত ।

তারপর আমরা যেই position এ ভেলু insert হবে সেখান থেকে পরের ভেলু গুলো একঘর করে সরিয়ে দিব ।

arr[size + 1] = arr[i]

একটি কথা মনে রাখবেন এখানে একঘর করে সরাচ্ছি মানে এই নয় যে যেই position এ insert হবে সেটা ফাকা থাকবে । ওখানেও আগের ভেলুই থাকবে । এখন আমরা এটাকে আপডেট করে দিব ।

arr[pos] = value

এটা একটা টেকনিক ছিল যেখানে n টাইম সময় নিবে । জেতা অনেক সময় একটু সমস্যা করে ফেলতে পারে । আর একটা টেকনিক হচ্ছে

২/ আমরা যেখানে বা যেই পজিশনে insert করব সেখানকার ভেলু টা একদম লাস্ট ইনডেক্সে রিপ্লেস করে দিব এখন সেই পজিশনে নতুন ভেলু দিয়ে আপডেট করব । এখানে 1 টাইম সময় লাগবে । এটা সর্টিং এর ক্ষেত্রে ভাল না কারণ এলোমেলো করে ফেলবে । তবে সেটাকে আবার সুদরে নেওয়া সম্ভব ।

এই ছিল ২ ধরনের insertion.

Deletion:

1. যদি আমরা একদম লাস্টের ইনডেক্স টা ডিলিট করতে চাই তাইলে শুধু আমাদের আমাদের array size টা কমাই দিলেই হচ্ছে

    if(pos == size - 1) size--
   

2. যেকোনো জাইগার ইনডেক্স ডিলিট করতে চাইলে জেতা করতে পারেন সেঁতা হচ্ছে একটা লুপ চালাবেন জেটা positon + 1 থেকে সুরু হবে এবং সেস হবে size এ । তারপর জেতা করবেন সেঁটা হচ্ছে সব ভেলুকে একঘর করে পেছনে পাঠাবেন । অবশ্যয় size-- করবেন শেষে ।

Search:

1. linear search: প্রথম থেকে ধরে লাস্ট পর্যন্ত সার্চ করলে তাকে লিনিয়াল সার্চ বলে । এটা করার জন্য লুপ চালিয়ে খুঁজে বের করে আনতে পারি । অবশ্যয় চেকিং রাখবে যে ইউজার ভুল কিছু দিচ্ছে না জেটা আক্সিস্ট করে না । সেঁতা করার জন্য একটা ফ্ল্যাগ রাখতে পার জেতার ইনিশিয়াল ভেলু হবে ০ । কিছু খুঁজে পাইলে ১ । বিঃদ্রঃ এক্ষেত্রে n গুন টাইম লাগবে । এবং sorted হতে হবে না । একাধিক ডাটা থাকতে পারে একি নামে বা Id তে ।

2. Binary search: sorted হতে হবে । এই সার্চ করা হয় array মিডেল পয়েন্ট ধরে ধরে ।

   

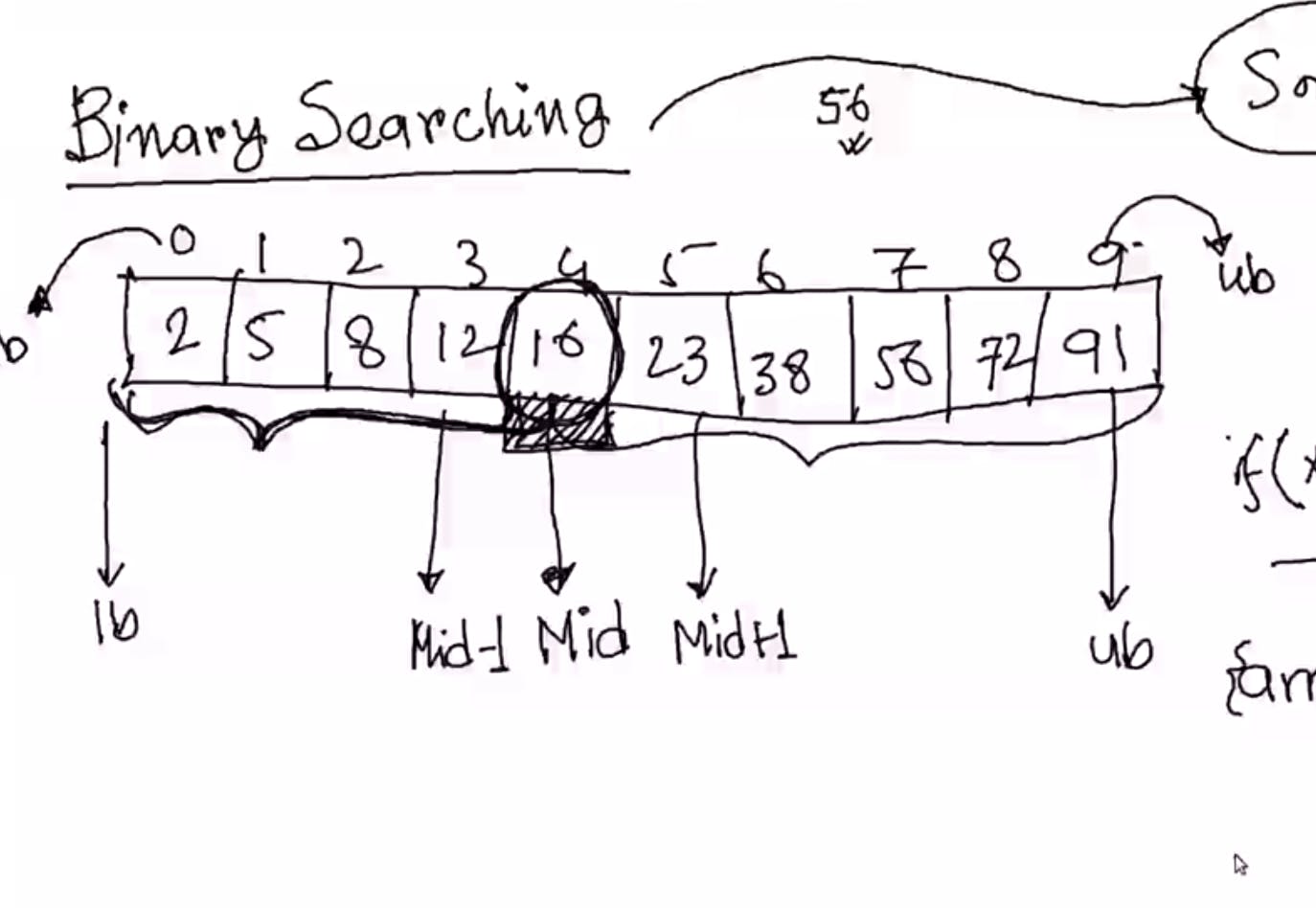
void binarySearch(int arr[], int x, int lb, int ub){
  if(lb <= up){
       int mid = (lb + lb) / 2;
       if(x == arr[mid]) return mid;
       else if(x > arr[mid]) binarySearch(arr,x, mid + 1, ub);
       else binarySearch(arr, x, lb, mid - 1)
    } else {
        return -1
    }
}

// fn call
binarySearch(arr, checkValue, 0, size - 1)

Sorting

---

bubble sorting:x

#include <bits/stdc++.h>
using namespace std;
int main(){
    int arr[] = {1, 3, 6, 3, 8, 1, 9, 3, 0};
    int size = (sizeof(arr) / sizeof(arr[0]));
    for (int i = 1; i < size; i++){
        for (int j = 0; j < size - 1; j++){
            if (arr[i] > arr[j + 1]){
                swap(arr[j], arr[j + 1]);
                // ------------- or-------------
                // int temp = arr[j];
                // arr[j] = arr[j + 1];
                // arr[j + 1] = temp;
            };
        }
    }
// print 
    for (int i = 0; i < size; i++){
        cout << arr[i] << endl;
    }

    return 0;
}

sorting with optimisation:

#include <bits/stdc++.h>
using namespace std;
void printArr(int arr[], int size){
    for (int i = 0; i < size; i++){
        cout << arr[i] << " ";
    }
    cout << endl;
}
int main(){
    int arr[] = {14, 11, 1, 2, 5, 4};
    int size = (sizeof(arr) / sizeof(arr[0]));
    for (int i = 1; i < size; i++){
        int flag = 0;
        for (int j = 0; j < size - i; j++){
            if (arr[j] > arr[j + 1]){
                swap(arr[j], arr[j + 1]);
                flag = 1;
            };
            printArr(arr, size);
        }
        cout << endl;
        if (flag == 0) break;
    }
    // print
    // printArr(arr, size);
    return 0;
}